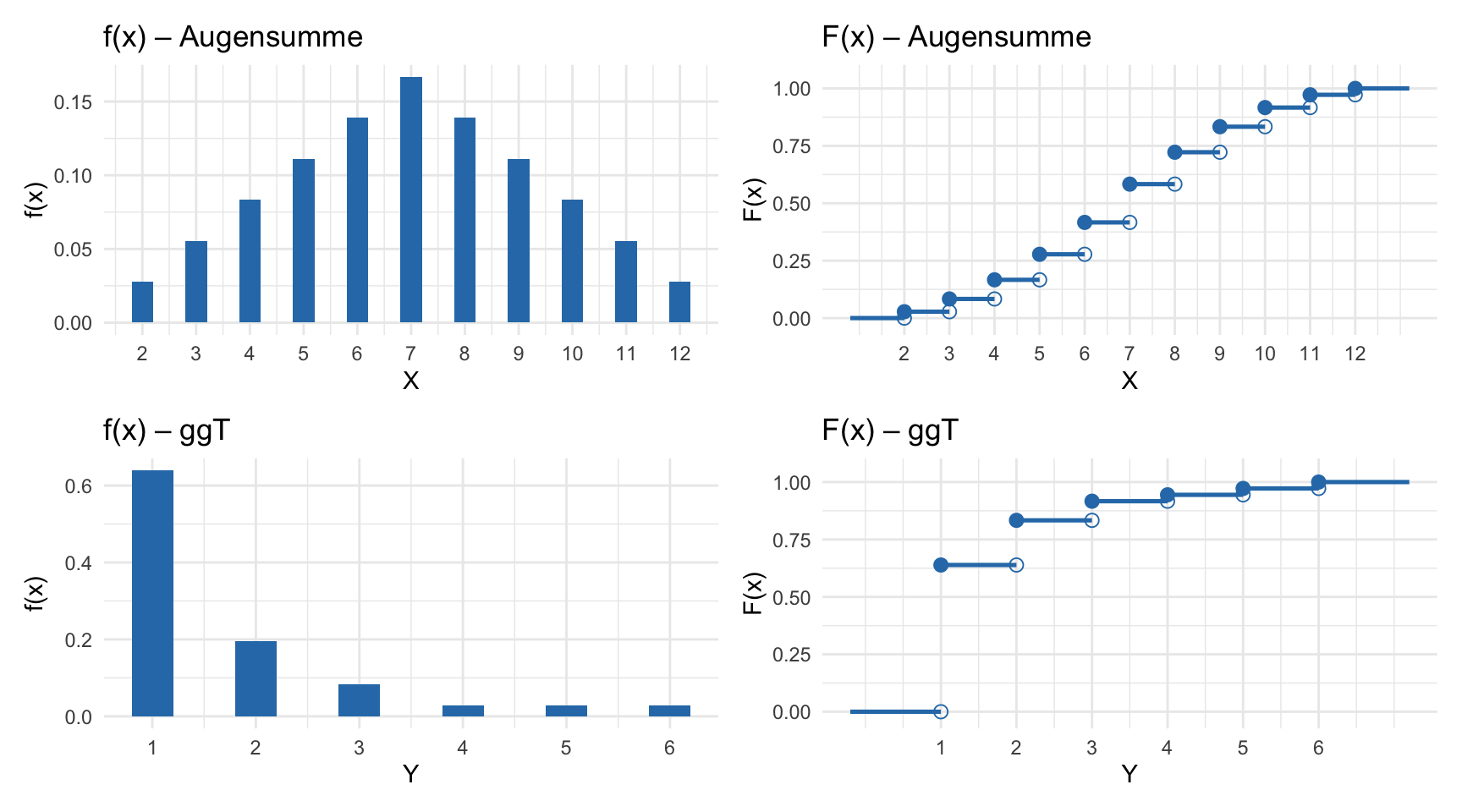
a) Sowohl \(X\) als auch \(Y\) sind diskrete Zufallsvariablen, da beide nur diskrete Werte, d.h. eine endliche Menge von Ausprägungen, annehmen können.
b) Es ist \(A = (X > 8)\) oder äquivalent \(A = (X \geq 9)\).
c) Ordnet man die Augenpaare \((a_1, a_2)\) in der Reihenfolge \((1,1), (1,2), \ldots, (1,6), (2,1), \ldots, (2,6), \ldots, (6,6)\) an, so lauten die dazugehörenden Ausprägungen von \(X\):
\[2, 3, 4, 5, 6, 7,\ 3, 4, 5, 6, 7, 8,\ 4, 5, 6, 7, 8, 9,\ 5, 6, 7, 8, 9, 10,\ 6, 7, 8, 9, 10, 11,\ 7, 8, 9, 10, 11, 12\]
Die Wahrscheinlichkeiten der möglichen Ausprägungen von \(X\) lauten:
| \(f(x)\) |
\(\tfrac{1}{36}\) |
\(\tfrac{2}{36}\) |
\(\tfrac{3}{36}\) |
\(\tfrac{4}{36}\) |
\(\tfrac{5}{36}\) |
\(\tfrac{6}{36}\) |
\(\tfrac{5}{36}\) |
\(\tfrac{4}{36}\) |
\(\tfrac{3}{36}\) |
\(\tfrac{2}{36}\) |
\(\tfrac{1}{36}\) |
Ordnet man die Augenpaare in derselben Reihenfolge, so lauten die Ausprägungen von \(Y = \text{ggT}(a_1, a_2)\):
\[1, 1, 1, 1, 1, 1,\ 1, 2, 1, 2, 1, 2,\ 1, 1, 3, 1, 1, 3,\ 1, 2, 1, 4, 1, 2,\ 1, 1, 1, 1, 5, 1,\ 1, 2, 3, 2, 1, 6\]
Die Wahrscheinlichkeiten der möglichen Ausprägungen von \(Y\) lauten:
| \(f(y)\) |
\(\tfrac{23}{36}\) |
\(\tfrac{7}{36}\) |
\(\tfrac{3}{36}\) |
\(\tfrac{1}{36}\) |
\(\tfrac{1}{36}\) |
\(\tfrac{1}{36}\) |
d) Der Erwartungswert von \(X\) ergibt sich aus den Ausprägungen \(x_k\) und den dazugehörenden Wahrscheinlichkeiten \(f(x_k)\) gemäss:
\[\begin{align}
E(X) &= \sum_{k=1}^{11} x_k \cdot f(x_k) \\
&= 2 \cdot \frac{1}{36} + 3 \cdot \frac{1}{18} + \cdots + 12 \cdot \frac{1}{36} = 7
\end{align}\]
Dies lässt sich auch ohne Rechnung einsehen: Da die Wahrscheinlichkeitsfunktion symmetrisch bezüglich der Ausprägung \(x_6 = 7\) ist, muss dies der Erwartungswert von \(X\) sein.
Die Varianz von \(X\) ergibt sich als:
\[\begin{align}
\text{Var}(X) &= E\!\left[(X - E(X))^2\right] = \sum_{k=1}^{11}(x_k - 7)^2 \cdot f(x_k) \\
&= (2-7)^2 \cdot \frac{1}{36} + (3-7)^2 \cdot \frac{1}{18} + \cdots + (12-7)^2 \cdot \frac{1}{36} \\
&= \frac{35}{6} \approx 5.833
\end{align}\]
Der Erwartungswert von \(Y\) ergibt sich als:
\[\begin{align}
E(Y) &= \sum_{k=1}^{6} x_k \cdot f(x_k) \\
&= 1 \cdot \frac{23}{36} + 2 \cdot \frac{7}{36} + \cdots + 6 \cdot \frac{1}{36} = \frac{61}{36} \approx 1.694
\end{align}\]
Und die Varianz von \(Y\) ergibt sich als:
\[\begin{align}
\text{Var}(Y) &= \sum_{k=1}^{6}\left(y_k - \frac{61}{36}\right)^2 \cdot f(x_k) \\
&= \left(1 - \frac{61}{36}\right)^2 \cdot \frac{23}{36} + \left(2 - \frac{61}{36}\right)^2 \cdot \frac{7}{36} + \cdots + \left(6 - \frac{61}{36}\right)^2 \cdot \frac{1}{36} \\
&= \frac{1859}{1296} \approx 1.434
\end{align}\]